Модуль math для математических вычислений

Вместе с установкой интерпретатора Python вы получаете большой набор готовых инструментов, собранных в стандартной библиотеке Python. Модули, входящие в неё, считаются неотъемлемой частью языка, что позволяет не устанавливать дополнительные пакеты и решать самые разные задачи: математические вычисления, генерация случайных чисел, работа с датой и временем, и много другое.

Среди всего многообразия модулей стандартной библиотеки модуль math является незаменимым помощником, когда речь заходит о более сложных математических вычислениях, которые выходят за рамки базовых арифметических операций, рассмотренных ранее.

Для использования функций и констант из этого модуля его следует импортировать:

import math

Константы

Модуль math предоставляет несколько полезных математических констант.

Числа math.pi и math.e

Константы math.pi и math.e являются обычными числами с плавающей точкой (float):

print(f"Площадь круга c радиусом 5 равна {math.pi * 5 ** 2:.2f}") 
# Вывод: Площадь круга c радиусом 5 равна 78.54
print(f"Число Эйлера равно {math.e:.2f}")
# Вывод: Число Эйлера равно 2.72

С ними можно производить вычисления, сравнивать с другими числами и так далее.

Бесконечность

Положительная бесконечность math.inf, которая также создаётся конструкцией float("inf"), используется для представления очень больших значений, например, при сравнении чисел:

print(math.inf > 99 ** 999) 
# Вывод: True

 Можно также использовать -math.inf для отрицательной бесконечности:

print(-math.inf < -99 ** 999) 
# Вывод: True

Не число

«Не число» math.nan, которое также создаётся конструкцией float("nan"), используется для представления результата некорректных математических операций. Главная особенность math.nan заключается в том, что оно не равно ничему, даже самому себе. Это помогает отличить его от обычных чисел, включая ноль и бесконечность:

print(math.nan == math.nan)
# Вывод: False
print(math.nan < math.inf)
# Вывод: False

Возведение в степень и вычисление корня

Хотя оператор ** позволяет возводить в степень и извлекать корень, модуль math предоставляет отдельные функции для этих операций.

Извлечение корня

Функция math.sqrt() является специализированной функцией для вычисления квадратного корня. Она более читабельна для математических формул, чем использование конструкции x ** 0.5:

print(math.sqrt(81))
# Вывод: 9.0
print(81 ** 0.5)
# Вывод: 9.0

Аргумент этой функции должен быть неотрицательным числом. Попытка извлечь корень из отрицательного числа приведет к ошибке ValueError, так как результатом будет комплексное число, с которым модуль math не работает.

Возведение в степень

Основное отличие функции math.pow() от оператора ** и встроенной функции pow() заключается в том, что она всегда возвращает результат типа float:

print(math.pow(2, 3))
# Вывод: 8.0
print(2 ** 3)
# Вывод: 8
print(pow(2, 3))
# Вывод: 8

Также в отличие от встроенной функции pow(), функция из модуля math не может принимать третий аргумент для вычисления остатка от деления.

Округление чисел

Как мы уже говорили, для случаев, когда число ровно посередине между двумя ближайшими значениями (например, 2.5), встроенная функция round() использует банковскоеокругление, то есть значение округляются в сторону ближайшего чётного числа. Однако модуль math расширяет возможности округления чисел в Python.

Функция math.ceil() округляет число в большую сторону, а функция math.floor(), наоборот, в меньшую. Даже их названия в переводе с английского означают ceiling – потолок и floor – пол, то есть округление вверх и вниз:

print(math.ceil(3.5))
# Вывод: 4
print(math.floor(3.5))
# Вывод: 3

При этом результат обеих функций не зависит от того, является число чётным или нечётным.

Функция math.trunc() просто отбрасывает дробную часть числа:

print(math.trunc(7.3))
# Вывод: 7

Факториал

Мы уже рассматривали факториал числа n как пример рекурсивной функции, которая возвращает произведение всех целых чисел от 1 до этого числа n включительно:

def factorial(n: int) -> int:
    # Базовый случай: если n равно 0 или 1, возвращаем 1 и прекращаем рекурсию
    if n == 0 or n == 1:
        return 1
    # Рекурсивный случай: n! = n * (n - 1)!
    return n * factorial(n - 1)

Однако мы можем не писать эту функцию, а импортировать её из модуля math:

print(math.factorial(3))
# Вывод: 6

При этом функция math.factorial() работает только с целыми неотрицательными числами.

Логарифмы и экспонента

Логарифм является обратной операцией к возведению в степень. Например, так как 2³ = 8, то log₂8 = 3 (читается как «логарифм 8 по основанию 2»). То есть это показатель степени, в которую нужно возвести основание, чтобы получить заданное число.

Модуль math предоставляет несколько функций для вычисления логарифмов по разным основаниям, в том числе по основанию e (числу Эйлера). Такой логарифм называется натуральным логарифмом, и в математике его принято обозначать как ln x.

Если говорить о натуральных логарифмах, то нельзя не упомянуть об экспоненте e^x, которая является его обратной функцией, и для расчёта которой модуль math также предоставляет отдельную функцию.

Функция math.log() может вычислить логарифм по любому основанию, в том числе, 2, 10 или любое другое:

print(math.log(27, 3))
# Вывод: 3.0
print(math.log(8, 2))
# Вывод: 3.0
print(math.log(math.e))
# Вывод: 1.0

Функции math.log10() и math.log2() являются частными случаями функции math.log() и позволяют не указывать нужное основание, а сразу вычислить двоичный или десятичный логарифм:

print(math.log10(10))
# Вывод: 1.0
print(math.log2(32))
# Вывод: 5.0

Функция math.exp() вычисляет экспоненту от числа, то есть возводит число Эйлера (math.e) в переданную степень:

print(math.exp(1))
# Вывод: 2.718281828459045

При этом экспонента является обратной функцией для натурального логарифма. То есть ln e^x = x и e^ln(x) = x:

print(math.log(math.exp(2)))
# Вывод: 2.0
print(math.exp(math.log(2)))
# Вывод: 2.0

Тригонометрия

Тригонометрия изучает углы, стороны и их соотношения в треугольниках. Модуль math предоставляет основные функции для выполнения таких вычислений.

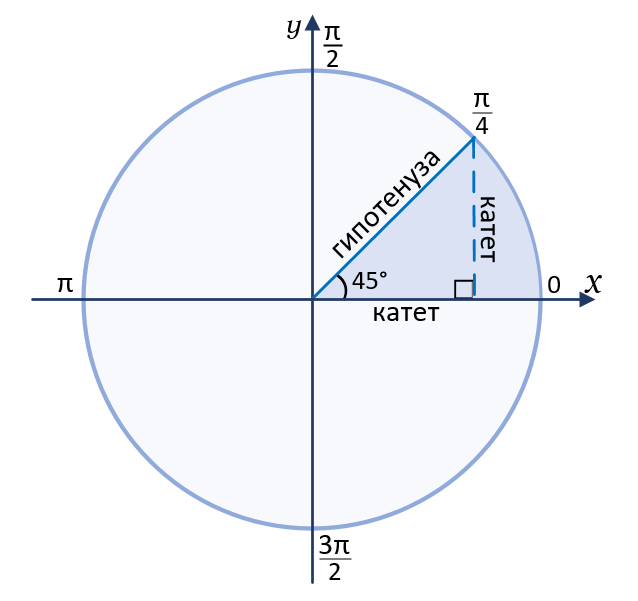
При работе с тригонометрическими функциями в Python (и в большинстве языков программирования) углы по умолчанию измеряются в радианах, а не в градусах. Эти две единицы измерения углов связаны с окружностью: полный оборот равен 360° или радиан, поэтому 1 радиан равен 360° / 2π ≈ 57.3°, а угол 45° соответствует π / 4 радиан.

Для перевода между этими системами модуль math предоставляет две функции:

• math.radians(degrees) – переводит градусы degrees в радианы.
• math.degrees(radians) – переводит радианы radians в градусы.

Так мы можем убедиться, что угол 180° равен числу π, а угол π / 2 соответствует 90°:

print(math.radians(180))
# Вывод: 3.141592653589793
print(math.degrees(math.pi / 2))
# Вывод: 90.0

Основные тригонометрические функции

Основные тригонометрические функции угла рассчитываются как соответствующее соотношение сторон в прямоугольном треугольнике, полученном при опускании перпендикуляра из точки на окружности до оси абсцисс.

Все эти функции принимают угол в радианах:
 

print(math.sin(math.radians(30)))
# Вывод: 0.49999999999999994
print(math.cos(math.pi))
# Вывод: -1.0
print(math.tan(math.pi / 4))
# Вывод: 0.9999999999999999

Из-за особенностей работы с числами с плавающей точкой в Python тригонометрические функции могут возвращать значения с минимальной погрешностью. Например, синус угла 30° на самом деле равен ровно 0.5, а тангенс угла π / 4 равен 1.

Обратные тригонометрические функции

Если основные функции находят соотношение сторон по углу, то обратные функции решают обратную задачу: они находят угол по известному соотношению сторон. Эти функции также часто называют аркфункциями.

Значение угла x для функций нахождения арксинуса math.asin() и арккосинуса math.acos() должны лежать в пределах от -1 до 1 включительно, в то время как функция арктангенса math.atan() может принимать любое значение:

print(math.asin(0.5))
# Вывод: 0.5235987755982989
print(math.acos(-1))
# Вывод: 3.141592653589793
print(math.atan(math.sqrt(3)))
# Вывод: 1.0471975511965976

Длина гипотенузы

Для вычисления длины гипотенузы прямоугольного треугольника с катетами x и y в модуле math есть функция math.hypot(x, y):

print(math.hypot(3, 4))
# Вывод: 5.0

Фактически это вычисление гипотенузы по теореме Пифагора, однако эта функция более устойчива к ошибкам округления, чем ручное вычисление math.sqrt(x ** 2 + y ** 2), особенно при очень больших или очень маленьких значениях x и y.

Примеры

Пример 1. Расчёт расстояния между двумя точками

Определение расстояния между точками с координатами (x₁; y₁) и (x₂; y₂) в двумерном пространстве (например, на карте в игре) сводится к применению теоремы Пифагора:

$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$

Здесь:

• (x₂ - x₁) – длина одного катета (разница по горизонтали);
• (y₂ - y₁) – длина второго катета (разница по горизонтали);
• d – гипотенуза (искомое расстояние).

Функция calculate_distance() принимает два кортежа с координатами точек и вычисляет расстояние между ними с помощью функции math.sqrt():

import math

def calculate_distance(point1: tuple, point2: tuple) -> float:
    """Рассчитывает расстояние между двумя точками.
    
    Параметры:
        point1: Координаты первой точки в виде кортежа (x, y).
        point2: Координаты второй точки в виде кортежа (x, y).
        
    Возвращает:
        Расстояние между точками point1 и point2.
    """
    # Распаковка кортежей
    x1, y1 = point1 
    x2, y2 = point2

    # Квадратный корень из суммы квадратов
    return math.sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2)


# Представляем точки как кортежи
point_a = (2.0, 5.0)  # (x1, y1)
point_b = (10.0, 11.0)  # (x2, y2)
print(f"Точка A: {point_a}, Точка B: {point_b}")

distance = calculate_distance(point_a, point_b)
print(f"Расстояние между точками: {distance:.2f}")

Обратите внимание, что пусть функции (и классы) следует отделять друг от друга и от остального кода двумя пустыми строками, то после строки с импортом достаточно оставить одну пустую строку.

Вывод:

Точка A: (2.0, 5.0), Точка B: (10.0, 11.0)
Расстояние между точками: 10.00

Пример 2. Обработка результатов вычислений

Математические вычисления часто требуют расчёт среднего арифметического. Для этого сумма элементов списка делится на его длину, однако длина пустого списка равна нулю, поэтому функция safe_mean() в таком случае возвращает константу math.nan, означающую «не число»:

import math

def safe_mean(data: list[int, float]) -> float:
    """Вычисляет среднее арифметическое списка чисел data.
    
    Параметры:
        data: Список чисел. Может быть пустым.
    
    Возвращает:
        NaN для пустого списка.
    """
    if not data:
        # Пустая последовательность: возвращаем math.nan ("Не число")
        return math.nan
    
    return sum(data) / len(data)


# Обычные данные
data1 = [10, 20, 30]
print(f"Среднее арифметическое списка {data1}: {safe_mean(data1)}")

# Пустой список
data2 = []
print(f"Среднее арифметическое списка {data2}: {safe_mean(data2)}")

Вывод:

Среднее арифметическое списка [10, 20, 30]: 20.0
Среднее арифметическое списка []: nan

Пример 3. Расчёт суммы инвестиций с непрерывным начислением процентов

При непрерывном начислении процентов проценты начисляются на сумму вклада за бесконечно малые промежутки времени, то есть капитализация происходит постоянно. Это означает, что процентная ставка применяется на постоянно растущую сумму, что приводит к более быстрому росту дохода, чем при периодической капитализации. Общая накопленная сумма на конец периода с процентами определяется по формуле:

$$ S = \text{e}^{(I \cdot T)} \cdot P $$

Здесь:

• e – число Эйлера;
• I – ставка непрерывных процентов в долях;
• T – срок вложения;
• P – сумма первоначальных вложений.

Функция continuous_compound() использует данную формулу и рассчитывает общую накопленную сумму, используя функцию math.exp:

import math

def continuous_compound(
    principal: float, 
    rate_fraction: float, 
    time_years: float
) -> float:
    """
    Рассчитывает финальную сумму при непрерывном начислении процентов.
    
    Параметры:
        principal: Cумма первоначальных вложений.
        rate_fraction: Ставка непрерывных процентов в долях.
        time_years: Cрок вложения.
    
    Возвращает:
        Общая накопленная сумма на конец периода с процентами.
    """
    return math.exp(rate_fraction * time_years) * principal

initial_investment = 100000.0  # Начальные вложения
print(f"Начальная сумма: {initial_investment} руб.")

annual_rate = 0.15  # Ставка 15%
print(f"Ставка: {annual_rate * 100} %")

time_horizon = 10.0  # Срок 10 лет
final = continuous_compound(initial_investment, annual_rate, time_horizon)
print(f"Через {time_horizon} лет сумма составит {final:.2f} руб.")

Вывод:

Начальная сумма: 100000.0 руб.
Ставка: 15.0 %
Через 10.0 лет сумма составит 448168.91 руб.

Итоги

• Модуль math предоставляет математические функции и константы для выполнения вычислений.
• В модуле math определены константы для числа Пи (math.pi), числа Эйлера (math.e), а также для бесконечности (math.inf) и не числа (math.nan).
• Модуль math предоставляет альтернативу для оператора возведения в степень ** – функцию math.pow(), а также функцию math.sqrt() для вычисления квадратного корня.
• Для округления числа в большую сторону используется функция math.ceil(), в меньшую – math.floor(), а для отбрасывания дробной части числа – math.trunc().
• Функция math.factorial() вычисляет факториал числа, то есть произведение всех целых чисел от 1 до этого числа включительно.
• Для вычисления логарифма предназначена основная функция math.log(), которая позволяет вычислять логарифм по любому основанию, но также есть специальные функции math.log2() и math.log10(), вычисляющие логарифм по основаниям 2 и 10 соответственно.
• Функция math.exp() возводит число Эйлера в степень переданного числа.
• При работе с тригонометрическими функциями в Python углы измеряются в радианах, а не в градусах. Для перевода градусов в радианы используется функция math.radians(), а радианов в градусы – функция math.degrees().
• Функции math.sin(), math.cos(), math.tan() вычисляют синус, косинус и тангенс угла соответственно.
• Функции math.asin(), math.acos() и math.atan() вычисляют арксинус, арккосинус и арктангенс угла соответственно.

Задания для самопроверки

1. Какое основание по умолчанию используется функцией math.log(), если второй аргумент base не указан? Как этот логарифм называется в математике?

2. Округлите число 2.5 сначала в большую, а затем в меньшую сторону, используя функции модуля math. Выведите оба округлённых числа на экран.

import math

print(math.ceil(2.5))
# Вывод: 3

print(math.floor(2.5))
# Вывод: 2

3. Напишите функцию calculate_area(radius), которая принимает радиус radius и использует константу math.pi для вычисления площади круга по формуле S = πr². Выведите на экран результат вызова функции для радиуса radius = 4, округлив его до двух знаков после запятой.

import math

def calculate_area(radius: int | float) -> float:
    return math.pi * math.pow(radius, 2)


area = calculate_area(4)
print(round(area, 2))
# Вывод: 50.27

4. Напишите функцию get_trigonometry(angle_degrees), которая принимает угол angle_degrees в градусах. Функция должна вычислить значения синуса, косинуса и тангенса этого угла (подумайте об единицах измерения) и вернуть полученные значения в виде словаря. Вызовите эту функцию для угла 30 градусов и выведите результат на экран.

import math

def get_trigonometry(angle_degrees: int | float) -> dict[str, float]:
    angle_radians = math.radians(angle_degrees)
    return {
        "sin": math.sin(angle_radians),
        "cos": math.cos(angle_radians),
        "tan": math.tan(angle_radians)
    }


results = get_trigonometry(30)
for key, value in results.items():
    print(f"{key} = {round(value, 2)}")
# Вывод: sin = 0.50
# Вывод: cos = 0.87
# Вывод: tan = 0.58

5. Вычислите значение следующего выражения, используя функции модуля math:

$$ e^{\lg5} + \sqrt{12} + \cos0.3 $$

Выведите результат на экран, округлив его до трёх знаков после запятой.

import math

result = math.exp(math.log10(5)) + math.sqrt(12) + math.cos(0.3)
print(round(result, 3))
# Вывод: 6.431